
|
Die torsionssteife Kiste
|

|

Der Hauptholm ist fü ein Lastenvielfaches von 2g ausgelegt worden.
Die Beplankung aus 1,5mm Sperrholz, ist von der statischen Seite nur für
die Torsinsaufnahme gedacht.
|
|
Rippenbauweise des Fügels
|

|

rechts im Bild ist der Hauptholm zu erkennen.
Auf ihn sind die Rippen aufgefädelt. Im inneren Fügel hat jede eine Länge von 2,10m und dabei nur ein Gewicht von je 100g.
In Belastungstests haben sie bewiesen das jede problemlos die geforderten 5 bis 6 Kg tragen können.
|
|
So ist der Kopf entstanden:
|

|
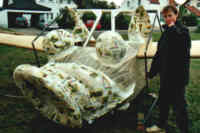
Den Rüssel, die Ohren und die Augen sind aus Maschendraht modelliert und mit vielen Schichten Seidenpapier beklebt worden.
Vielen Dank an meine Eltern...
Es ist genial geworden!
|
|
Bauweise des Rumpfes:
|

|

Der Rumpf besteht aus 10 elliptischen Spanten, die auch in der Fachwerkbauweise hergestellt wurden. Sie sind mit Längsgurten untereinander
verbunden.
Mit Kohlefaser wurden die Alurohre an der Gitterkonstruktion befestigt, die den Piloten und die Flügel getragen haben.
|
|
Rund um die Fügel:
|

|

Die Flügel sind für ein Lastenvielfaches von 2g ausgelegt worden.
d.H. sie halten eine Last von über 200 Kg.
Dabei wogen sie jeweils nur ca. 9 Kg !!!
|
|
extremste Leichtbauweise beim HLW!
|

|

So baut man ein Höhenleitwerk mit 2,60m Spannweite und 3,60m Länge wenn es ein Gewicht von nur 2 Kg haben soll.
Das es dabei noch Teilbar und sehr einfach Montierbar ist, setzt man einfach voraus, oder?
Profilierung: NACA 0006
|
Planung
Die Grundidee war, die Flugsau so zu bauen, dass sie einem Drachen ähnlich zu starten und zu fliegen ist.
Ein Ziel war es auch, sie wie eine lebendig gewordene Comic-Figur aussehen zu lassen. Der Pilot sollte möglichst in den Hintergrund treten,
damit die Sau richtig wirken kann.
Von Red Bull gab es auch einige Vorgaben an die man sich halten musste, wenn man an dem Flugtag am Wannsee teilnehmen wollte. So haben sie z.B. die
Spannweite auf 9 Meter begrenzt.
Die Größe der tragenden Fläche wollte ich von meinem (damaligen) Drachen, dem Impuls 14, übernehmen, denn das Startverhalten
war vorbildlich. Mit ca. 30 km/h fliegt er mit einer Zuladung von 65 Kg, dabei wiegt er selber nur ca. 30 Kg.
Da die
Re-Zahl ungefähr 1,2×10
6 ist, kann bei dem gewählten Profil E216 das c
a max
mit ca. 1,5 angesetzt werden (bei einem Anstellwinkel von 6°), ohne einen Strömungsabriss befürchten zu müssen. Mit Hilfe der Bedingung:
v
min=
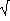
((2
·m
·g) / (
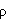 ·
·A
·c
a max))
kommt man auf ein maximales Gewicht von ca. 100 Kg. Da ich keine größere Lust auf eine umfassende Diät hatte, musste die Flugsau
noch in der Planungsphase eine Radikaldiät über sich ergehen lassen.
Dies schlägt sich in einer sehr extremen Bauweise nieder. Nahezu die komplette Sau wurde aus nur 3×4 mm dicken, teils vorgebogenen Kieferleisten
gebaut. Also feinstes 3D-Fachwerk mit 0,4 mm dickem Knotenpunktverstärkungen aus Sperrholz.
Nachdem ich die ersten 3-Seiten-Ansichten skizziert hatte, kamen auch schon die ersten Zweifel. Um bei einer Rumpfbreite von 1,6 m die 14 m²
Flügelfläche auf den 9 m Spannweite zu verteilen, musste die mittlere Flächentiefe ca. 2,10 m betragen. Das ließ sich mit den
ästhetischen Gesichtspunkten nicht vereinen. Die Lösung war eine geschwungene Form der Tragflächen. Dann kann man die große Tiefe
etwas kaschieren. Das Ganze hat aber einen großen Nachteil: Zum einen muss der Hauptholm jetzt in alle Richtungen gekrümmt und verjüngt
werden, zum Anderen wird es sehr aufwendig, die geplante Sperrholzbeplankung über eine gekrümmte Nasenleiste zu ziehen.
So, wie geht man jetzt vor, wenn man einen Bauplan für so ein Fluggerät entwickeln will?
|
Spannweite
|
9,00 m
|
|
Länge
|
6,30 m
|
|
Flügel-Fläche
|
14,00 m²
|
|
Höhenleitwerks-Fläche
|
4,50 m²
|
|
Rumpfbreite
|
1,60 m
|
|
Gesammthöhe
|
1,80 m
|
|
Gewicht
|
40 Kg
|

Zuerst habe ich den Grundriss der Tragflächen im AutoCAD (CAD-Programm) gezeichnet. Dabei habe ich versucht möglichst viele identische Rippen
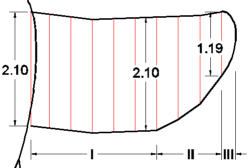
zu bekommen, damit die "Massen-" Produktion schneller von der Hand geht. Das erreicht man durch eine konstante Flächentiefe über eine möglichst großen Bereich (I).
Im Randbereich (II) hat jede Rippe eine andere Länge und im äußeren Bereich (III) ist eine Art Winglet (hochgebogenes Tragflächenende) gebaut.
Das gewählte Profil wurde für den Kopfflügel einer Ente entworfen und besitzt ein besonders hohes c
a max (maximaler Auftriebsbeiwert). Damit erkauft man sich auch
ein hohes c
m 0,25 (Drehmoment) aber dazu später mehr...

Der nächste Schritt ist der, das Profil (E216) auf die Rippen zu verteilen. Dabei wird es auf die Größe/ Länge jeder einzelnen Rippe skaliert. Jetzt
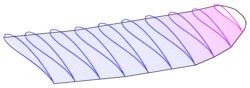
wird es in dem inneren Bereich (I) mit 6° angestellt und in dem Bereich (II) von
6° auf nur noch 2° verzogen. Der Sinn der Aktion ist eine Gutmütigkeit im Abriss- verhalten der Flächen zu erhalten.
Wenn die Strömung im überzogenen Flugzustand abreißt, dann soll sie bitte zuerst im inneren Bereich der Flächen abreißen.
Da die Wahrscheinlichkeit sehr groß ist, das die Strömung nicht auf beiden Seiten gleichzeitig abreißen wird, wäre die Gefahr, dass der Flieger sich sofort
um die Längsachse dreht sehr groß. Der noch vorhandene Auftrieb der anderen Seite mit dem großen Hebelarm würde ein großes Drehmoment erzeugen, welches
ein Abkippen über die Seite mit der abgerissen Strömung verursachen würde.

Wenn jetzt aber die Flächentiefe, Profillänge und der Anstellwinkel über die Tragfläche variiert wird, wie ermittelt man dann den möglichen Auftrieb?
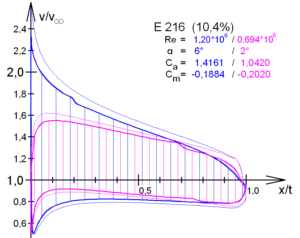
In dieser Grafik steckt die Lösung, auch wenn das für den "Laien" auf den ersten Blick nicht so ganz zu erkennen ist ;-)
Hier ist die Geschwindigkeits- verteilung über das Profil bei zwei verschiedenen Anstellwinkeln und
Re-Zahlen errechnet worden. Was kann man jetzt denn um Himmels
willen mit der Geschwindigkeits- verteilung anfangen???
Mit Hilfe der
Bernoullischen Gleichung
kann man die Geschwindigkeit in eine Druckverteilung umrechnen. Grundlage ist (unter gewissen Rand- bedingungen) die Tatsache,
dass die Summe aus Geschwindigkeitshöhe und Druckhöhe immer konstant bleibt.
Hat man das geschafft, so braucht man nur noch das Integral (die Fläche) der oberen und unteren Konturlinie zu bestimmen. Das Ergebnis ist der Auftriebsfaktor
c
a.
Später braucht man auch noch das erzeugte Drehmoment (um das Höhenleitwerk zu dimensionieren). Dazu trägt man den Druck der jeweiligen Position am Profil an,
muss aber darauf achten, dass der Vektor rechtwinklig zur Profiloberfläche gezeichnet wird.
Dabei ist es klar, dass die Größen und Verteilungen der Druckvektoren bei jedem Anstellwinkel anders aussehen.
Jetzt kann man die Vektoren nach den üblichen Methoden addieren. Die resultierende Kraft stellt dann den Auftrieb und den Luftwiderstand dar.

Üblicherweise wird sie in eine vertikale (c
a) und horizontale (c
w) Komponente aufgespalten. Der Angriffspunkt der vertikalen Komponente (Auftrieb) ist jetzt noch im wirklich wirkenden Punkt.
Da der Punkt aber mit jeder Änderung von Anstellwinkel und Geschwindigkeit seine Position verändert, führt man eine "feste" Position für den
Auftrieb ein. Diese Position ist bei 25% der Profillänge. Durch das Verschieben einer Kraft quer zu ihrer Wirkrichtung entsteht ein Drehmoment. Und dieses ist der
Beiwert c
m oder auch c
m 0,25.
Nachdem die Kräfte an den Profilen klar sind, kommt ein weiter Beweggrund ins Spiel, dieses Profil zu wählen:
Die Profildicke ist recht groß und beträgt 10,4%. Bei einer Profillänge von 2,10 m eine hat das Profil eine Dicke von 21,8 cm. Somit läßt sich ein

Hauptholm bauen, der meinen extremen Gewichtsansprüchen und auch der statischen Last gerecht werden kann.
Woher weiß man überhaupt, wie stark der Hauptholm werden muss?
Dazu braucht man die Verteilung des Auftriebs über die Tragfläche. Um die zu errechnen gibt es eine ganze Menge "wilder" Formeln, ich habe
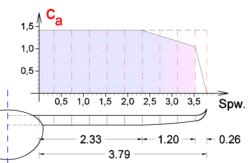
mir aber das Leben an dieser Stelle etwas leichter gemacht (deshalb wurde auch später eine gesunde Reserve eingeplant).
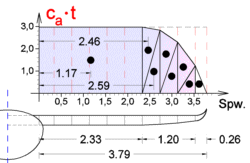
Also man nehme sich die c
a Werte und trage sie über die Spannweite auf. Dann multipliziert man sie mit der Tiefe (Rippenlänge) an der jeweiligen Stelle.
Das Ergebnis nimmt man als Auftriebsverteilung auch wenn es nach aerodynamischen Gesichtspunkten so noch nicht ganz stimmt...
Unser gesuchtes Biegemoment (zur Ermittlung der Hauptholm- abmessung) ergibt sich aus folgender Formel:
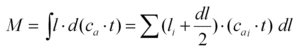
Die Formel sieht mal wieder schlimmer aus, als sie eigentlich ist. Es werden nur die Teilflächen mit dem Hebelarm vom Nullpunkt bis zu
ihrem Teilschwerpunkt multipliziert und anschließend
aufaddiert. Trapeze werden der Einfachheit halber in zwei Dreiecke aufgeteilt und immer darauf geachtet, das der Schwerpunkt bei Dreiecken 1/3 von der Basis bzw. 2/3 von der Spitze entfernt liegt...
Exemplarisch wird hier kurz das Biegemoment aus dem Rechteck (1) und dem zweiten Dreieck (3) berechnet:
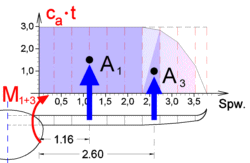
M
(1+3)= (c
a1·t
1)
·(dl
1)
2/2
+ (c
a3·t
3)
·dl
3/2
·(dl
1+2/3
·dl
3)
M
(1)= 1,416
· 2,10[m]
· (2,33[m])
2/2 = 8,07[m
3]
M
(3)= 1,291
· 1,91[m]
· 0,40[m]/2
· (2,33[m]+2/3
· 0,40[m]) = 1,28[m
3]
=> M
(1+3)= 8,07 + 1,28 = 9,35 [m
3]
=> M
(ges) = 11,43 [m
3]
Das Ergebnis ist eine Zahl mit einer etwas komischen Einheit. Um auf unsere geliebte Einheit [Nm] zu kommen, müssen wir noch mit der Luftdichte und dem Quadrat der Geschwindigkeit
multiplizieren....
Um dies auch physikalisch zu untermauern, nehmen wir die Formel der minimalen Fluggeschwindigkeit von weiter oben, mit der die max Startmasse berechnet wurde. Diese
formen wir so um, dass wir als Ergebnis den Ausdruck m
·g (dem Auftrieb F
A) erhalten.
F
A = m
·g = c
a· t
· b
·
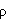
/2
· v
2
und da
M = F
A · b/2
bei einer Rechteckverteilung ist, ergibt sich:
M = (c
a· t
· b
·
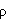
/2
· v
2)
· b/2
bzw.
M = (c
a· t
· b
2/2)
·
(
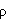
/2
· v
2) = [m
3]
· ([Kg/m
3]
· [m/s]
2) =
[Kg
· m
2/s
2]
und da [N] = [Kg
· m/s
2] ist, haben wir die [Nm] erreicht, und alles ist wieder im Lot...
In einer Höhe von 0 m über NN ist die Luftdichte
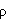
= 1,225 Kg/m
3.
Und Berlin liegt nicht gerade auf einem Berg...
M = 11,43
·
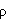
/2
· v
2 = 11,43
· 1,225/2
· v
2 = 7,00
· v
2 [Nm]
Somit bleibt nur noch die Frage übrig, welche Geschwindigkeit hier eingesetzt werden soll. Zurück zum Problem, den Hauptholm dimensionieren zu müssen. Und damit die Frage,
was wäre denn das Ungünstigste für den Holm? Na ja, je größer v wird, desto größer wird auch M. Also nehmen wir die maximale Geschwindigkeit, die wir erwarten.
Die ergibt sich wiederum aus den ungünstigsten Randbedingungen.
Zum einen ist es die Geschwindigkeit, die ich zu Fuß beim Startvorgang erreichen werde. Das sind mindestens
30 Km/h - nicht wundern,
ohne Fluggerät, an dem ich mich im letzten Endspurt festhalten kann, erreiche ich die sicherlich nicht...
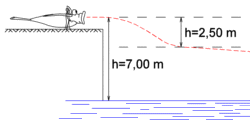
Dann nehmen wir mal an, das ich nach dem Start ca. 2,50 m durchsacken könnte, ohne das der Auftrieb diesen "Fall" bremsen würde.
Somit würde sich eine zusätzliche vertikale Geschwindigkeitskomponente (freier Fall) von
v
s =
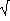
(2
·g
·h)=
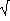
(2
·9,81
·2,50)= 7,00 [m/s]
<=>
25,21 [km/h]
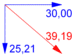
ergeben. Mit dem Pythagoras errechnen wir dann die daraus resultierende Geschwindigkeit:
v=
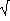
(v
h2 + v
s2)=
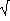
(30
2 + 25,21
2)=
39,19 [Km/h]
<=> 10,88 [m/s]
Damit haben wir jetzt alle Zahlen um das maximale Biegemoment zu bestimmen:
M= 7,00
· 10,88
2= 828,62 [Nm]
Wie hoch, bzw. dick muss der Hauptholm jetzt werden?
W
erf= M
vorh /
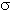 zul
zul
verrät uns das erforderliche Trägheitsmoment, wenn
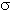 zul
zul bekannt ist. Und das ist es,
sobald man sich für einen Werkstoff entschieden hat. Bei mir sollte es Holz, genauer Fichte werden. Denn ich hatte von einem Schreinermeister die Zusage, von ihm auf Maß geschliffenes Holz
zu bekommen. Darunter ein dickes Fichtebrett mit sehr feiner und gerader Maserung, das auch schon 10 Jahre abgelagert war!!!
Das vorhandene Holz konnte problemlos in die Sortierklasse "S13" eingruppiert werden, der Sicherheit und Systemreserven willens habe ich es dann doch nur in die Klasse "S10"
zugeordnet.
=>
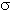 zul
zul= 10 [N/mm
2]
<=> 1 000 [N/cm
2]
W
erf= 828,62
· 100 / 1 000 = 82,862 [cm
3]
Die allgemeine Formel zur Ermittlung des Widerstandsmomentes aus der Geometrie eines Trägers lautet:
W
y=
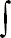
z dA
Auf Grund der Linearität dieser Gleichung kann man sie für einfache geometrische Körper anpassen.
Somit lassen sich bei gegebener Höhe (Profildicke) die notwendigen Breiten errechnen.
Bei mir soll ein so genannter doppel-T Träger zum Einsatz kommen. Das ist die effektivste Form, wenn man Gewicht und Festigkeit bei gleicher Bauhöhe (20 cm) ins Verhältnis setzt, wie die unten
stehende Tabelle zeigt.
| Form |
 |
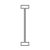 |
 |
 |
| Wy [cm3] |
200,00 |
98,08 |
785,40 |
375,42 |
| A [cm2] |
60,00 |
20,50 |
314,16 |
87,18 |
| Wy / A= |
3,33 |
4,78 |
2,50 |
4,31 |
Für einen doppel-T Träger lässt sich die Formel zur Errechnung des Widerstandsmomentes auch wie folgt ausdrücken, wenn nur die Gurte zur Festigkeitsrechnung
herangezogen werden:
W
y= A
1 · z
1 + A
2 · z
2
Bei gleichen Abmessungen des Zug- und Druckgurtes (A
1 = A
2) ist der Schwerpunkt auf h/2 und damit auch
(z
1 = z
2).
=> W
y= 2
· A
1 · z
1
Wie groß ist jetzt die nötige Gurtfläche A
1 bzw.
der Schwerpunktsabstand z
1?
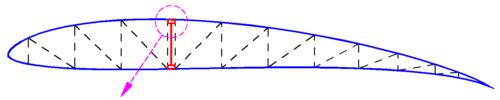
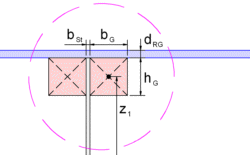
Die Holmgurte sollten quadratischen Querschnitt haben, darum ist b
G=h
G
=> A
1= 2
· h
G · h
G
z
1= h
ges / 2 - d
RG - h
G / 2
h
ges= 210 cm
· 10,4%= 21,84 cm
d
RG = 0,3 cm (Dicke des Rippengurtes)
Damit wird:
W
y= 82,862= 2
· 2
· (h
G)
2 · (21,84/2 - 0,3 - h
G/2)
<=> 0= (h
G)
3 - 21,24
·(h
G)
2 + 41,431
=> h
G= b
G= 1,45 [cm] (gewählt 1,5 x 1,5 cm)
Somit sind die Stärken der Leisten bestimmt, die den Zug- bzw. Druckgurt des Hauptholms bilden.
In dem Bereich des Flächenanschlusses (Übergang Flächen- Rumpf) bleiben die Gurte auf 15 x 15 mm. In Richtung Randbogen werden sie konisch geschliffen, dass sie am
Randbogen nur noch 5 x 5 mm Stärke haben.
Als Steg wird ein 1,5 mm starkes Sperrholz (mit Faserrichtung vertikal!!!) gewählt.
Bei Belastungsversuchen hat sich ergeben, dass es im Holm ohne regelmäßige Beulsteifen bei dem extrem dünnen Steg zum Struktur-
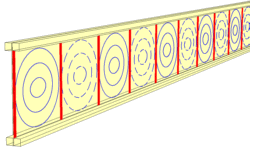
versagen kommt. Also wurden alle 20 cm Beulsteifen vorgesehen, die den Steg in quadratische Beulfelder teilt. Diese Beulfelder sind in dem Bild als eine Art von Höhenlinien
dargestellt. Dabei beult ein Feld nach vorne und das nächste Feld nach hinten, dies ist mit den durchgezogenen bzw. gestrichelten Linien symbolisiert.
Damit ist der Hauptholm fertig ausgelegt.
Der nächste Punkt auf der "Liste" ist die
Dimensionierung des Höhenleitwerks.
Unter Dimensionierung verstehe ich im ersten Anlauf die Ermittlung des notwendigen Leitwerk- Volumens. Damit ist nicht etwa gemeint, wieviel "Liter" Luft das Leitwerk hat,
sondern wieviel Leitwerksfläche [m
2] in welchem Abstand zu dem Neutralpunkt in der Tragfläche angeordnet werden muss.
Im zweiten Anlauf ist dann wirklich die Dimensionierung der (Holz-) Bauteile gemeint.
wird fortgesetzt!!!
letzte Aktualisierung
am: 06.07.2006










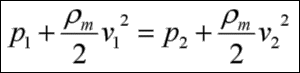
 Nachdem ich die ersten 3-Seiten-Ansichten skizziert hatte, kamen auch schon die ersten Zweifel. Um bei einer Rumpfbreite von 1,6 m die 14 m²
Flügelfläche auf den 9 m Spannweite zu verteilen, musste die mittlere Flächentiefe ca. 2,10 m betragen. Das ließ sich mit den
ästhetischen Gesichtspunkten nicht vereinen. Die Lösung war eine geschwungene Form der Tragflächen. Dann kann man die große Tiefe
etwas kaschieren. Das Ganze hat aber einen großen Nachteil: Zum einen muss der Hauptholm jetzt in alle Richtungen gekrümmt und verjüngt
werden, zum Anderen wird es sehr aufwendig, die geplante Sperrholzbeplankung über eine gekrümmte Nasenleiste zu ziehen.
Nachdem ich die ersten 3-Seiten-Ansichten skizziert hatte, kamen auch schon die ersten Zweifel. Um bei einer Rumpfbreite von 1,6 m die 14 m²
Flügelfläche auf den 9 m Spannweite zu verteilen, musste die mittlere Flächentiefe ca. 2,10 m betragen. Das ließ sich mit den
ästhetischen Gesichtspunkten nicht vereinen. Die Lösung war eine geschwungene Form der Tragflächen. Dann kann man die große Tiefe
etwas kaschieren. Das Ganze hat aber einen großen Nachteil: Zum einen muss der Hauptholm jetzt in alle Richtungen gekrümmt und verjüngt
werden, zum Anderen wird es sehr aufwendig, die geplante Sperrholzbeplankung über eine gekrümmte Nasenleiste zu ziehen. zu bekommen, damit die "Massen-" Produktion schneller von der Hand geht. Das erreicht man durch eine konstante Flächentiefe über eine möglichst großen Bereich (I).
Im Randbereich (II) hat jede Rippe eine andere Länge und im äußeren Bereich (III) ist eine Art Winglet (hochgebogenes Tragflächenende) gebaut.
zu bekommen, damit die "Massen-" Produktion schneller von der Hand geht. Das erreicht man durch eine konstante Flächentiefe über eine möglichst großen Bereich (I).
Im Randbereich (II) hat jede Rippe eine andere Länge und im äußeren Bereich (III) ist eine Art Winglet (hochgebogenes Tragflächenende) gebaut.
 wird es in dem inneren Bereich (I) mit 6° angestellt und in dem Bereich (II) von
6° auf nur noch 2° verzogen. Der Sinn der Aktion ist eine Gutmütigkeit im Abriss- verhalten der Flächen zu erhalten.
wird es in dem inneren Bereich (I) mit 6° angestellt und in dem Bereich (II) von
6° auf nur noch 2° verzogen. Der Sinn der Aktion ist eine Gutmütigkeit im Abriss- verhalten der Flächen zu erhalten.
 In dieser Grafik steckt die Lösung, auch wenn das für den "Laien" auf den ersten Blick nicht so ganz zu erkennen ist ;-)
In dieser Grafik steckt die Lösung, auch wenn das für den "Laien" auf den ersten Blick nicht so ganz zu erkennen ist ;-)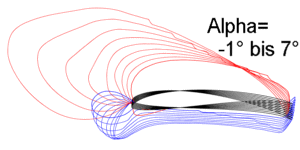
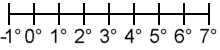
 Üblicherweise wird sie in eine vertikale (ca) und horizontale (cw) Komponente aufgespalten. Der Angriffspunkt der vertikalen Komponente (Auftrieb) ist jetzt noch im wirklich wirkenden Punkt.
Da der Punkt aber mit jeder Änderung von Anstellwinkel und Geschwindigkeit seine Position verändert, führt man eine "feste" Position für den
Auftrieb ein. Diese Position ist bei 25% der Profillänge. Durch das Verschieben einer Kraft quer zu ihrer Wirkrichtung entsteht ein Drehmoment. Und dieses ist der
Beiwert cm oder auch cm 0,25.
Üblicherweise wird sie in eine vertikale (ca) und horizontale (cw) Komponente aufgespalten. Der Angriffspunkt der vertikalen Komponente (Auftrieb) ist jetzt noch im wirklich wirkenden Punkt.
Da der Punkt aber mit jeder Änderung von Anstellwinkel und Geschwindigkeit seine Position verändert, führt man eine "feste" Position für den
Auftrieb ein. Diese Position ist bei 25% der Profillänge. Durch das Verschieben einer Kraft quer zu ihrer Wirkrichtung entsteht ein Drehmoment. Und dieses ist der
Beiwert cm oder auch cm 0,25. Hauptholm bauen, der meinen extremen Gewichtsansprüchen und auch der statischen Last gerecht werden kann.
Hauptholm bauen, der meinen extremen Gewichtsansprüchen und auch der statischen Last gerecht werden kann. mir aber das Leben an dieser Stelle etwas leichter gemacht (deshalb wurde auch später eine gesunde Reserve eingeplant).
mir aber das Leben an dieser Stelle etwas leichter gemacht (deshalb wurde auch später eine gesunde Reserve eingeplant).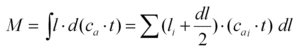
 ihrem Teilschwerpunkt multipliziert und anschließend
aufaddiert. Trapeze werden der Einfachheit halber in zwei Dreiecke aufgeteilt und immer darauf geachtet, das der Schwerpunkt bei Dreiecken 1/3 von der Basis bzw. 2/3 von der Spitze entfernt liegt...
ihrem Teilschwerpunkt multipliziert und anschließend
aufaddiert. Trapeze werden der Einfachheit halber in zwei Dreiecke aufgeteilt und immer darauf geachtet, das der Schwerpunkt bei Dreiecken 1/3 von der Basis bzw. 2/3 von der Spitze entfernt liegt...
 Dann nehmen wir mal an, das ich nach dem Start ca. 2,50 m durchsacken könnte, ohne das der Auftrieb diesen "Fall" bremsen würde.
Dann nehmen wir mal an, das ich nach dem Start ca. 2,50 m durchsacken könnte, ohne das der Auftrieb diesen "Fall" bremsen würde.




 Die Holmgurte sollten quadratischen Querschnitt haben, darum ist bG=hG
Die Holmgurte sollten quadratischen Querschnitt haben, darum ist bG=hG versagen kommt. Also wurden alle 20 cm Beulsteifen vorgesehen, die den Steg in quadratische Beulfelder teilt. Diese Beulfelder sind in dem Bild als eine Art von Höhenlinien
dargestellt. Dabei beult ein Feld nach vorne und das nächste Feld nach hinten, dies ist mit den durchgezogenen bzw. gestrichelten Linien symbolisiert.
versagen kommt. Also wurden alle 20 cm Beulsteifen vorgesehen, die den Steg in quadratische Beulfelder teilt. Diese Beulfelder sind in dem Bild als eine Art von Höhenlinien
dargestellt. Dabei beult ein Feld nach vorne und das nächste Feld nach hinten, dies ist mit den durchgezogenen bzw. gestrichelten Linien symbolisiert.